Simˈpōzēəm
 Olav Jones, Deputy Director General, Insurance Europe
The outcome of the trilogue discussions between the European Parliament, Council and Commission on the Omnibus II Directive will determine the success of the EU’s Solvency II regime. The stakes are high. The insurance industry plays a vital role in society but also — with around €7,700 billion of assets under management and €1,100 billion of new premiums to invest annually — in the growth and economic stability of the European economy.
A well designed Solvency II framework should provide a safe regulatory regime that captures insurers’ real risks. Solvency II must also allow insurance companies to continue to contribute to long-term investment and to economic growth, and to offer long-term products so that customers can plan their retirement. These three roles are currently at risk. A working group of the Bank for International Settlements, chaired by Peter Praet of the European Central Bank, reached a similar conclusion:
Olav Jones, Deputy Director General, Insurance Europe
The outcome of the trilogue discussions between the European Parliament, Council and Commission on the Omnibus II Directive will determine the success of the EU’s Solvency II regime. The stakes are high. The insurance industry plays a vital role in society but also — with around €7,700 billion of assets under management and €1,100 billion of new premiums to invest annually — in the growth and economic stability of the European economy.
A well designed Solvency II framework should provide a safe regulatory regime that captures insurers’ real risks. Solvency II must also allow insurance companies to continue to contribute to long-term investment and to economic growth, and to offer long-term products so that customers can plan their retirement. These three roles are currently at risk. A working group of the Bank for International Settlements, chaired by Peter Praet of the European Central Bank, reached a similar conclusion:
“A related concern is whether life insurers and pension funds can maintain a long-term investor perspective. […] A partial retreat of institutional investors from the long-term and/or illiquid segment of the credit market could reduce the private and social benefits the sector generates through long-term investing, and the extent to which it mitigates the pro-cyclicality of the financial system.”1It is concerns over the serious and unintended consequences of Solvency II for long-term investment and products, and debate over how to address those concerns that are the main cause of delay in finalising the framework. The solutions under discussion have strong justifications. It is therefore vital to clarify misunderstanding of how they affect the valuation of liabilities.
The problem with current market consistency
 A market-consistent approach has been chosen as the basis for Solvency II because it is a framework that captures many of the elements needed by a solvency regime. For example, it takes into account the size and timing of expected liability cashflows, captures the impact of embedded options and guarantees, and captures asset/liability mismatches, etc.
However, we should never forget that the fundamental goal of Solvency II is to create a risk-based solvency regime that provides strong customer protection and risk management incentives. Its goal was not to implement a market-consistent approach; this was a means to an end, not the end in itself. Therefore, if the existing market-consistent framework methodology does not work for insurance business, it needs to be improved and adapted. Arguing, as some have, that improvements cannot be made purely because they are not in line with current market-consistent methodology is letting the tail wag the dog.
We should also not forget that market consistency is a theoretical framework designed to model how the real world works. As with all theoretical frameworks, in trying to model that world it makes a number of simplifying assumptions. It is vital to check whether these assumptions are fit for purpose and — if not — to make improvements.
A market-consistent approach has been chosen as the basis for Solvency II because it is a framework that captures many of the elements needed by a solvency regime. For example, it takes into account the size and timing of expected liability cashflows, captures the impact of embedded options and guarantees, and captures asset/liability mismatches, etc.
However, we should never forget that the fundamental goal of Solvency II is to create a risk-based solvency regime that provides strong customer protection and risk management incentives. Its goal was not to implement a market-consistent approach; this was a means to an end, not the end in itself. Therefore, if the existing market-consistent framework methodology does not work for insurance business, it needs to be improved and adapted. Arguing, as some have, that improvements cannot be made purely because they are not in line with current market-consistent methodology is letting the tail wag the dog.
We should also not forget that market consistency is a theoretical framework designed to model how the real world works. As with all theoretical frameworks, in trying to model that world it makes a number of simplifying assumptions. It is vital to check whether these assumptions are fit for purpose and — if not — to make improvements.
Four assumptions challenged
Four key assumptions made by a current market-consistent framework do not hold and must be addressed to ensure Solvency II works as intended. We analyse each assumption below. The first assumption of the classical framework is that all liabilities can be priced in the market. This assumption does not hold for insurance because there is no liquid market for most insurance liabilities and therefore for liability valuations. To cope with this shortcoming of the classical market-consistent framework a Risk Margin was developed for Solvency II to capture the uncertainty in future liability cashflows in a way that is in line with a market-consistent approach. Second, the classical framework holds that the market price is always appropriate. The underlying assumption here is that markets are always rational. However, during economic crises we have seen prices that are either not reliable due to very limited participants in the market and/or that cannot be justified on an economic basis (e.g. AAA bond spreads increasing to 200bp). For companies with fully liquid liabilities this may not matter because – whether or not the price is valid – they are fully exposed to it. For insurance companies with very few highly liquid liabilities, the excessive volatility in the market does not reflect the solvency position, given the limited vulnerability to such short-term volatility. If this issue is not addressed, many insurance companies could exit long-term business. The proposed introduction of a Counter-Cyclical Premium (CCP) in Solvency II creates a mechanism that can cope with extreme and temporary market pricing in an appropriate way. A third assumption is that all assets are always available for sale, implying that the credit risk for insurers is always driven by movement in spreads and actual defaults are irrelevant. However, we contend that where insurance companies can protect themselves from the impact of spread movements (because of features of their liabilities), then it is actual defaults that impact their balance sheet and risk exposure not the movement in spreads. This matters because, as many studies have shown, there is little or no direct connection between volatility in current spreads (and therefore values) and long-term default experience2. The Matching Adjustment mechanism is needed to ensure that the correct risk is measured for insurance companies both in terms of the valuation of their balance sheet to avoid artificial volatility and, in measuring the credit SCR, to ensure it reflects default risk and not spread risk. Lastly, a classical market-consistent framework assumes that the market can provide a risk-free curve to value liabilities of any duration. In reality the market can only reliably provide data for the risk-free curve for a limited duration (e.g. up to about 20 years for the euro and as low as about ten years for some European countries). Insurance liabilities are often well beyond these periods. The current Solvency II proposal includes an Extrapolation methodology to extend the interest rate curve beyond the point where the market is deep and liquid so that liabilities of all maturities can be valued.Why does this matter so much?
[caption id="attachment_56005" align="alignleft" width="330"]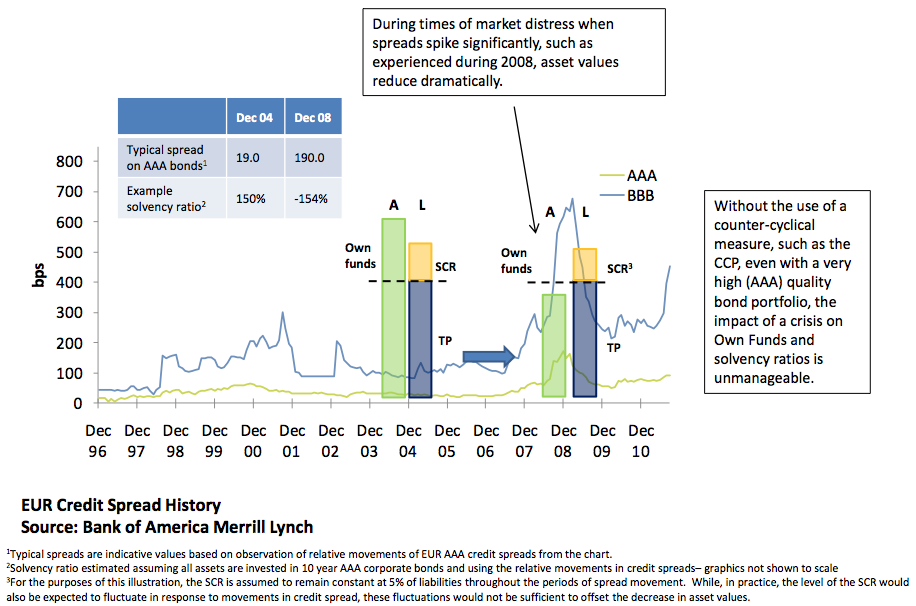 Figure 1: Impact of extreme spread movements during distressed market[/caption]
The first assumption has been addressed in the Solvency II measurement framework. Solutions to the others are currently under discussion, so it is worth looking at some examples that illustrate how — if not dealt with — they can create unmanageable artificial volatility in the own funds and solvency.
We have constructed a very simplified insurance company with a balance sheet based on 10 year bonds backing a portfolio of 10 year guarantees.
In Figure 1 we estimated the impact on this company of the distressed market period experienced in 2008. Without a CCP mechanism such a company, even one investing in the highest quality bonds, would experience unmanageable volatility in own funds and solvency ratios due to the temporary spike in spreads.
[caption id="attachment_56004" align="alignright" width="337"]
Figure 1: Impact of extreme spread movements during distressed market[/caption]
The first assumption has been addressed in the Solvency II measurement framework. Solutions to the others are currently under discussion, so it is worth looking at some examples that illustrate how — if not dealt with — they can create unmanageable artificial volatility in the own funds and solvency.
We have constructed a very simplified insurance company with a balance sheet based on 10 year bonds backing a portfolio of 10 year guarantees.
In Figure 1 we estimated the impact on this company of the distressed market period experienced in 2008. Without a CCP mechanism such a company, even one investing in the highest quality bonds, would experience unmanageable volatility in own funds and solvency ratios due to the temporary spike in spreads.
[caption id="attachment_56004" align="alignright" width="337"]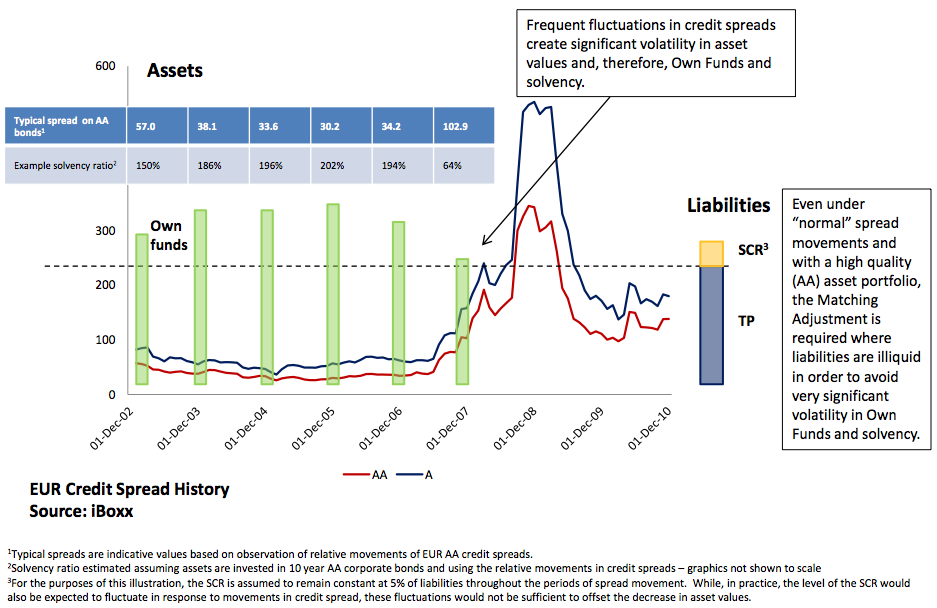 Figure 2: Impact of spread movements during normal times[/caption]
In Figure 2 we have estimated the impact of more normal volatility in spreads outside a crisis period based on actual experience from 2002 to 2007. Here we have assumed the company invests in high-quality AA bonds. This is volatility that would not normally trigger a CCP but would create significant volatility in own funds and therefore solvency. Where the nature of liabilities protects the company from the impact of spread volatility, an appropriately designed Matching Adjustment would avoid this artificial volatility.
Figure 2: Impact of spread movements during normal times[/caption]
In Figure 2 we have estimated the impact of more normal volatility in spreads outside a crisis period based on actual experience from 2002 to 2007. Here we have assumed the company invests in high-quality AA bonds. This is volatility that would not normally trigger a CCP but would create significant volatility in own funds and therefore solvency. Where the nature of liabilities protects the company from the impact of spread volatility, an appropriately designed Matching Adjustment would avoid this artificial volatility.
The impact on the valuation of claims liabilities has been misunderstood
The Matching Adjustment ensures that where liabilities are not exposed to the risk of movements in credit spread, the changes in asset values due to spread movements do not create artificial volatility in own funds. In order to illustrate how this mechanism works, it is easiest to consider the value of liabilities as having two components:- The best estimate value of projected claims and any profit sharing.
- The impact of any risk mitigation features incorporated within the liabilities.
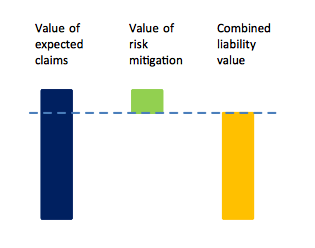 Figure 3: Split of total liability values between value of expected claims and value of risk mitigation[/caption]
Risk-mitigation techniques are used throughout the insurance industry and they are commonly considered separately from the value of the liabilities (as is the case for reinsurance or hedging programmes). However, where risk-mitigation features are incorporated within the product design (i.e., being able to hold backing assets to maturity or being able to pass asset losses on to customers), the combined position must be considered.
When these components are considered in isolation, it becomes clear that while the first component is dependent purely on expected claims experience (and hence has nothing to do with the backing assets unless there are profit-sharing arrangements), the value of the second component is significantly impacted by the assets backing the liability.
[caption id="attachment_54680" align="alignright" width="292"]
Figure 3: Split of total liability values between value of expected claims and value of risk mitigation[/caption]
Risk-mitigation techniques are used throughout the insurance industry and they are commonly considered separately from the value of the liabilities (as is the case for reinsurance or hedging programmes). However, where risk-mitigation features are incorporated within the product design (i.e., being able to hold backing assets to maturity or being able to pass asset losses on to customers), the combined position must be considered.
When these components are considered in isolation, it becomes clear that while the first component is dependent purely on expected claims experience (and hence has nothing to do with the backing assets unless there are profit-sharing arrangements), the value of the second component is significantly impacted by the assets backing the liability.
[caption id="attachment_54680" align="alignright" width="292"]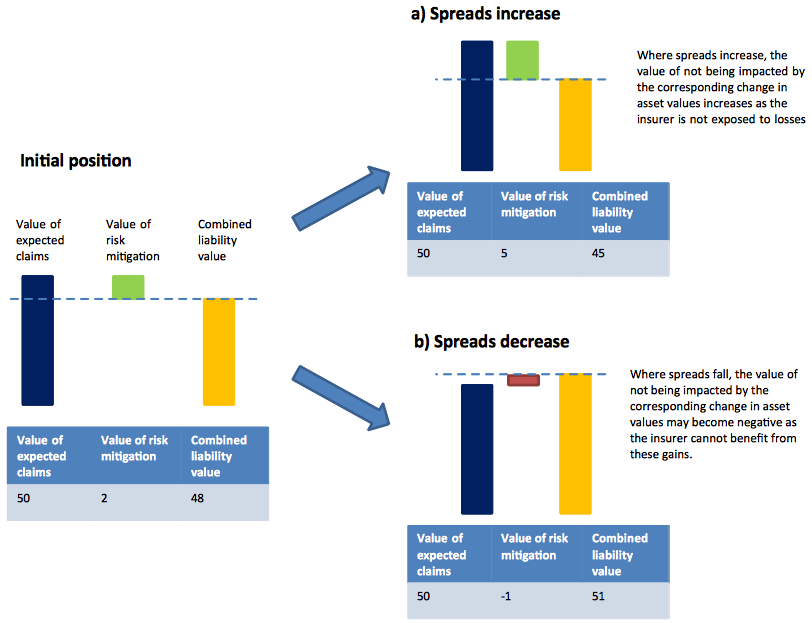 Figure 4: Changes in components of total liability value under different market conditions[/caption]
As with other risk-mitigation tools, the value of the risk mitigation varies depending on the position of the risk it is mitigating. For example, a reinsurance arrangement protecting an insurer against catastrophe losses becomes significantly more valuable when a catastrophe is occurring. In the same way, the value of this risk mitigation is highly related to the current value of the assets: if spreads widen, leading to unrealised losses on assets, then the value of this risk-mitigation feature of the liabilities increases. Conversely, as shown in the diagram below, where spreads narrow and the value of unrealised gains increases, the value of the risk mitigation may become negative if the insurer is not able to capitalise on these unrealised gains.
The mechanism currently proposed by the Commission for implementing the Matching Adjustment is to include the value of this mitigation by adjusting the discount rate used for the valuation of the expected claims. This has the result of combining the two components — value of claims and value of risk mitigation — into one single total liability figure.
This had led some commentators to think that inclusion of the Matching Adjustment is somehow distorting the value of the claims. It is not. It is simply ensuring that the risk-mitigation value of the liability features that insulate the company from losses due to spread movements on the assets is valued in a reasonable way.
Figure 4: Changes in components of total liability value under different market conditions[/caption]
As with other risk-mitigation tools, the value of the risk mitigation varies depending on the position of the risk it is mitigating. For example, a reinsurance arrangement protecting an insurer against catastrophe losses becomes significantly more valuable when a catastrophe is occurring. In the same way, the value of this risk mitigation is highly related to the current value of the assets: if spreads widen, leading to unrealised losses on assets, then the value of this risk-mitigation feature of the liabilities increases. Conversely, as shown in the diagram below, where spreads narrow and the value of unrealised gains increases, the value of the risk mitigation may become negative if the insurer is not able to capitalise on these unrealised gains.
The mechanism currently proposed by the Commission for implementing the Matching Adjustment is to include the value of this mitigation by adjusting the discount rate used for the valuation of the expected claims. This has the result of combining the two components — value of claims and value of risk mitigation — into one single total liability figure.
This had led some commentators to think that inclusion of the Matching Adjustment is somehow distorting the value of the claims. It is not. It is simply ensuring that the risk-mitigation value of the liability features that insulate the company from losses due to spread movements on the assets is valued in a reasonable way.







Several questions/remarks that I hope the other contributors will be able to answer:
Isn’t it precisely because the stakes are high as mentioned in the introduction that the regulation has to be strict?
It is possible to choose to ignore the market when it behaves “ irrationally” but how about forced sales during these periods of “market irrationality” (due to mass lapse for instance eg Korea during the Asian crisis in 1998)? Mark consistency is bit like democracy it is a poor system but it is the best we have.
This feels like a plea to bend the SII principles in order to fit old products into the new framework how about adapting products to the new regime. Empirical evidence in financial services and other heavily regulated industries such as pharmaceutical, telecom… suggest that the negative impact of regulation is generally overestimated ex-ante and that market innovation contribute to reduce if not cancel out the negative consequences that had been anticipated.
Also there is no mention of extrapolation it would have been interesting to see how the starting point for the extrapolation of the curve at 20 years for the EURO can be justified on the basis that the euro denominated bond market is not deep and liquid enough when the extrapolation for GBP starts at 50 years . For memory the EURO denominated bond market is the biggest in the world (EUR200b issued a month and EUR 17,000b of outstanding debt).