Simˈpōzēəm
 This paper, originally published by Groupe Consultatif on 6 December 2012, purely reflects an actuarial view about the implicit assumptions and consequences of a market consistent valuation framework. It does not state an opinion about whether market consistency is a bad or good concept, nor does it recommend to use or not to use market consistency as a principle for regulation.
This paper, originally published by Groupe Consultatif on 6 December 2012, purely reflects an actuarial view about the implicit assumptions and consequences of a market consistent valuation framework. It does not state an opinion about whether market consistency is a bad or good concept, nor does it recommend to use or not to use market consistency as a principle for regulation.
Introduction: why are we writing such a paper
This paper summarises the key principles underlying market consistent valuations of assets and liabilities. Its underlying aim is to help actuaries and others best interpret the concept of ‘market consistency’ in contexts where several possible valuation approaches are or might be proposed. The intention of this paper is to focus on the underlying generic meaning to assign to this concept rather than on any technical meaning that might be given to it by any specific piece of legislation or regulation. Legislative and regulatory frameworks often involve political or pragmatic compromises. Meanings assigned to terms by such frameworks may diverge from their underlying generic meaning in order to implement such compromises. The concept of market consistent valuations has been popularised by inclusion of the concept in the proposed Solvency II Directive for the European insurance industry, but some of the ways in which the concept is likely to be implemented by Solvency II may include such compromises. This paper has been prepared by a Task Force of the Groupe Consultatif Actuariel Europeen, a body representing actuarial associations in different European jurisdictions. One of the reasons for preparing this paper is to provide a framework for addressing differences of opinion over what might constitute a market consistent valuation for some types of liabilities. The paper aims to characterise where there is broad agreement on the generic meaning to ascribe to a ‘market consistent’ valuation. Thus the paper is purely educational and does not aim to lobby for any economic or political interest. It is likely to be followed by other papers exploring some cases where views diverge, highlighting which views might be reasonably deemed to be ‘market consistent’ and in what circumstances.Definitions: what does market consistency mean?
As explained in Kemp (2009), there are a range of definitions for a market consistent value (MCV), a term that is in large part also consistent with how many use the term fair value1. The definition we adopt here is the one preferred in Kemp (2009), i.e.:A market consistent value of an asset or liability2 is its market value, if it is readily traded on a market at the point in time that the valuation is struck, and, for any other asset or liability, a reasoned best estimate of what its market value would have been had it been readily traded at the relevant valuation point.Several points flow from this definition. The most obvious is that the extent to which it is possible to identify a unique market consistent value depends on the extent to which the asset or liability is ‘readily traded’ on a market. Conventionally, this is understood to require the market in the relevant asset or liability to be deep, liquid and transparent. The more the market in an asset or liability exhibits these characteristics the more reliable is the ascribing of a market consistent value to it. Conversely, the more the market in the relevant asset or liability does not exhibit such characteristics the more judgement will typically be required to come up with a market consistent value and the more scope there is for reasonable divergence of opinion over exactly what this value should be. Several other corollaries follow because economic theory indicates that a market that is deep, liquid and transparent is unlikely to permit other than fleeting instances of pure arbitrages. A pure arbitrage is a strategy that involves a sure profit with zero initial outlay, for example if we can buy an asset at one price and simultaneously sell it at a higher price3. Moreover an essential prerequisite of a market being liquid (and deep) is that it should involve very modest transaction costs (for material but not excessively large transactions). This means that we can assume that such markets adhere to the principle of no arbitrage4, otherwise known as the law of one price. Kemp (2009) also refers to this principle as the axiom of contemporaneous value continuity, to highlight that it tells us next to nothing about how values might evolve through time (i.e. it only relates to values that are contemporaneous with each other) and can be interpreted as implying not only that identical assets or liabilities should have identical values (the law of one price) but also that nearly identical ones should have nearly identical values. The principle of no arbitrage implies that market consistent values (for assets and liabilities traded in deep, liquid and transparent markets in which there are negligible transaction costs and other market frictions) should adhere to the following axioms: Existence At any point in time there should exist a value5 for any specific asset or liability. More generally we can think of any asset or liability or any combination of them as involving specific ‘pay‐offs’ (with the pay‐offs, i.e. the cash flows the asset or liability or combination generates, being generally positive for an asset and generally negative for a liability). Thus to any pay‐off, a, it is assumed that we can ascribe a market consistent value V(a). Uniqueness To have this value V(a) unique it is additionally required to have a complete market available. That means that any asset or liability to be valued should be reproducible (later we will call them replicable) by some assets or liabilities traded in this market. Additivity and scalability For any two payoffs, a and b, and for any scalar value, k, the market consistent value of payoff k(a + b) (by which we mean k times the combination of the cash flows arising from and a and b in tandem) must satisfy:
V(k(a+b))=k(V(a)+V(b))
More precisely, we may assert that this is how market consistent valuations should work and we can then in part interpret deep, liquid and transparent markets as being ones whose market values actually adhere to such principles. For example, if a market is not transparent then it will generally be difficult or impossible to identify an objective market value for anything traded on it, probably stopping any observed market value from being unique and arbitrage opportunities become possible. If the above equation is adhered to then we need V(–a)=–V(a), which means that if market values are to be unambiguous and universally agreed upon then transaction costs must be negligible or some convention that effectively ignores them, such as always using mid prices, must be adopted (as otherwise there may scope for differences of opinion over exactly where within the bid‐offer range the market price of a given pay‐off should be set). By letting k tend to zero we can also conclude that the market consistent value of a set of zero cash flows is zero.Replication
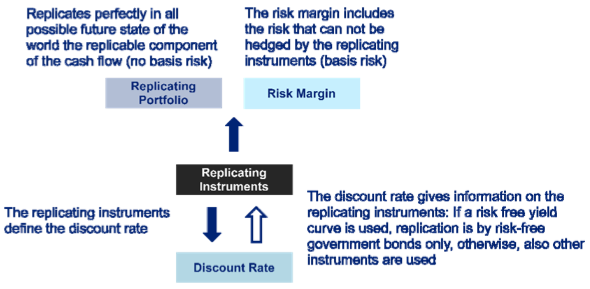
The extension of such principles to assets or liabilities that are not traded on a market relies very heavily on the principle of replication. Suppose, for example, we have a liability, a, that is not traded in a deep, liquid and transparent market but it can be perfectly replicated by an financial instrument6, b, that is. By perfectly replicated we mean that its cash flows are exactly the same (except in sign) for all possible future states of the world during the entire duration of the cash flows, so b=–a and thus a=–b. Hence the market consistent value of such a liability, V(a)=V(–b)=-V(b), i.e. the two have the same market consistent value except for a change of sign. Alternatively, we may re‐formulate our definition of market consistency around the idea of replication, defining the market consistent value of, say, an untraded liability to be the market value of the replicating traded financial instrument (multiplied by –1). However, strictly speaking, this requires us to make assumptions about how market values of such assets behave so it is probably more theoretically justifiable to treat the principle of replication as a consequence of how we have defined market consistency rather than as the way in which we might define market consistency.Incomplete Markets
Of course, we will rarely be able to replicate perfectly any particular set of asset and liability cash flows using financial instruments traded on such markets. Instead, replication will only in general be approximate. Markets in which the full range of possible financial instruments we might wish to be able to observe for such purposes are called complete markets. In real life, markets are incomplete, i.e. there is not the full range of instruments readily traded on them to allow all assets or liabilities to be valued using the principle of replication. Where assets or liabilities cannot be perfectly replicated by reference to financial instruments readily traded on the market then there will be scope for differences of opinion over what might be their market consistent value. This corresponds to the inherent uncertainty in how the missing assets in an incomplete market would trade Thus market consistent values need not necessarily to be unique. However, there will generally be limits on how far market consistent valuations might reasonably diverge from each other, especially if the replication is nearly perfect. As we have already noted, we not only need identical cash flows to be valued identically, we also need nearly identical cash flows to be valued nearly identically.Discounting
A common actuarial activity is to calculate the present value of a series of cash flows. This involves discounting future cash flows at suitable rates of interest back to the present. How might we discount a given series of untraded future liability cash flows in a market consistent manner? Following the above principles, we identify a series of cash flows of financial instruments on the market that replicate in all essential respects the liability cash flows and then apply the principle of replication. This in practice is usually implemented by deriving from the cash flows on the market a yield curve which when applied to these cash flows replicates (as far as possible) their market values. This yield curve is then applied to the relevant liabilities. If for example only credit risk free government bonds are used for replication, then the yield curve for discounting corresponds to the risk free government yield curve. In general, the implied discount rate depends on the portfolio to be valued and corresponds to the averaged discount rate that is implied by the set of financial instruments that replicate the cash flow of the insurance liabilities. Importantly, ‘in all essential respects’ requires the risks expressed by the cash flows of the financial instruments to correspond to the risks expressed by the liability cash flows. For example, if the liability cash flows are credit risk sensitive then the appropriate yield curve to use would be one that is derived from financial instruments with exposure to a corresponding amount and type of credit risk. We have largely glossed over exactly how we might define a market and how we might observe a market price for any given financial instrument traded on such a market. These topics are explored further in Kemp (2009). An important point in practice is to realise that the world is not really entirely black or white, i.e. with it being clear whether an appropriate market does or does not exist. Instead, usually it involves shades of grey with few markets being unequivocally deep, liquid and transparent but with many approximating to some extent this ideal.Mathematical and Economical Consequences
Cash Flows
Insurance and pension contracts give rise to future uncertain cash flows. Additional cash flows will be needed to get and hold capital to serve the supervisory requirements. For insurers and pension institutions to be able to produce all these future cash flows, they have to invest premiums and contributions as well as capital in financial and non‐financial assets. In a market consistent valuation standard, the market consistent value (MCV) of liabilities corresponds to the cost of producing the resulting cash flows using tradable assets7. For the MCV to be reliable, the cost of the financial instruments that are used for producing the liability cash flows for the purpose of valuation has to be able to be determined in a reliable manner. This implies that the financial instruments used have to have reliable market prices and have to be traded in a deep, liquid and transparent market. We call the set of financial instruments available for valuation the space of replicating instruments. This does not imply that the holder of the liability actually has to invest in the replicating instruments. They are rather used so that the MCV is reliable. For insurance contracts and similarly for pensions and other financial contracts, the uncertain future cash flows to be valued consist of all relevant in‐ and outflows, usually including premiums or contributions, investment returns, reimbursements, claims and benefit costs, administration costs, management fees, overheads, commissions, capital costs, etc. The purpose of the valuation determines which cash flows should be used and the risk exposures (e.g. credit quality characteristics) that should be ascribed to these cash flows. For example, different assumptions may be relevant depending on whether the purpose of the valuation is to estimate a transfer value or to determine a run‐off value. Also potentially dependent on the valuation purpose is the extent to which overhead costs, commissions and other expenses should be included in the cash flows. For example, for some purposes it may be appropriate to base administration costs on usual market rates whilst for other purposes it may be more appropriate to use undertaking specific rates. It is important to note that market consistent valuation does not aim to arrive at some ‘intrinsic value’ of a financial instrument. Instead, it aims to determine the cost of producing a given set of cash flows. It is therefore not relevant to a market consistent valuation whether market prices of assets are perceived to deviate from some believed ‘true’ intrinsic values. What is important for a market consistent valuation is the cost for the holder of a liability to reproduce (i.e. replicate) the liability cash flows using assets that are traded in a deep, liquid and transparent market. Perceived market failures or deviations from believed ‘true’ intrinsic values can be an indication to buy (or sell) an asset for a value‐investor, but are not themselves relevant to determining the cost of reproducing the liability cash flows.Best Estimate plus Risk Margin
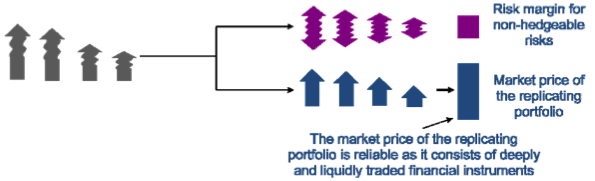
Two consequences apply if perfect replication is not possible. Firstly, there may be a greater range of possible portfolios that might be considered to constitute a suitable (approximate) replicating portfolio and secondly, the value of such an (approximate) replicating portfolio may deviate from that value of the liability which seems most appropriate for a given valuation purpose. This deviation stems purely from the variability or uncertainty of the cash flows rather than from their expected value8, which means that it describes risk. It is generally handled using one of two different conceptual frameworks which are equivalent in substance but involve different ways of characterising this risk and therefore need different sets of valuation conventions. In the first conceptual framework, the cash flows of the liabilities are unbundled into two parts, the part that can be (exactly) replicated and the remainder (i.e. the non‐replicable part). The deviation, which relates merely to the non‐replicable liabilities, may then be modelled as a risk margin for the non‐replicable risks added to a so‐called best estimate (or expected value) for the non‐replicable cash flows. In theory unbundling the replicable parts of the liability cash flows from non‐replicable parts (sometimes also called hedgeable and non‐hedgeable risks9) in this way requires stochastic independence of the hedgeable and non‐hedgeable risks. The overall market consistent value placed on the liabilities is then the market value of the replicating portfolio of the hedgeable part (unique) plus a best estimate for the non‐hedgeable part of the liabilities (unique, but might be zero) plus the risk margin for the non‐hedgeable part of the liabilities (depends on how the risk margin is defined, thus not unique as a general rule)10. In the second conceptual framework the best estimate is included within the replicating component, with the replication being ‘as good as possible’ given the range of possible replicating portfolios. The risk margin then corresponds to some measure of how inaccurate the overall replication might prove to be, i.e. with the non‐replicable risk minimized by choosing a replicating portfolio which is optimal according to some distance measure11. The overall MCV placed on the liabilities is then the market value of this (overall, approximate) replicating portfolio plus a risk margin because the replicating portfolio is not a perfect match or hedge for the liabilities. In this approach the choice of a ‘best possible’ replication portfolio depends on the optimising distance measure, which creates a conceptual difference to the first approach where after unbundling the cash flows the replication strategy is straight forward. The following picture illustrates the second conceptual framework approach: Either way, because there is no single right way of identifying the ‘most accurate’ approach to replication there is no single right way of calculating a market consistent value. Some other constraints need to be imposed, e.g. by the regulator12, to indicate how to select between alternative possible choices of (approximate) replicating portfolios or how to unbundle cash flows. For the two conceptual frameworks described above to be consistent, the best estimate in the first framework ought to be defined in a manner consistent with how the ‘best’ (approximate) replicating portfolio is defined in the second framework, but this is not necessarily always the case for all regulatory frameworks. In general, for regulatory purposes the non‐hedgeable risk will need to be buffered by capital or the equivalent over the lifetime of the cash flows. It depends on the underlying accounting framework whether and how far such a buffer has to be allocated to the technical provisions (usually in form of an additional (risk) margin) or to equity13. A common way of quantifying margins applied to the best estimate is by reference to the expected cost of servicing this capital buffer. The idea behind this is to include in the replication not only the cash flows of the liability but also the cash flows to the provider of the required capital (cost of capital). Such margins are often also called risk margins again and are consistent with the risk margin approaches described above. The risk margin in general depends on both the liabilities to be valued and the space of replicating instruments. In particular, if the replicating instruments are credit‐risky or contain other risks (e.g. valuation uncertainty in case of illiquid instruments) not present in the liabilities then these risks should be reflected in the risk margin.Replicating instruments
At the core of market consistent valuation is the choice of the space of replicating instruments. Once the space of replicating instruments and the purpose of the valuation are chosen, the MCV is essentially determined (for replicable liabilities). The space of replicating instruments also determines the split into the replicable and non‐replicable component of the liability. A (replicating) valuation is in general determined by two choices: the replication approach and the cash flows to be valued. While the choice of the cash flows depends on the purpose of the valuation, the choice of the replication determines the valuation per se. For the replication, essentially two decisions have to be taken:- Whether the replication is static or dynamic and
- The financial instruments used to replicate the cash flows.
Market Consistency and regulation
Market consistent valuation is a key element of some new regulatory frameworks, such as Solvency II. There is general agreement on many aspects of what constitutes a market consistent value. However, in some areas there is (inherent) scope for differences of opinion. This is because it is never entirely clear how assets or liabilities that are not (currently) readily traded on a market would be priced if such a market in them were to exist. For example, suppose we have some untraded insurance liabilities that are variable in nature. Our first port of call to determine their market consistent value would be to identify corresponding readily traded assets that replicate in all essential respects their cash flow characteristics, here including how they might vary in the future. But suppose that they have elements that cannot be replicated by readily traded assets. We must then infer how these liability elements would trade were an active market in them to exist or we must develop some other methodology to handle the parts of the cash flows that cannot be replicated with traded instruments. Solvency II tackles the inherent uncertainty this introduces by mandating that the non‐replicable components of the liabilities are valued by referring to best estimate probabilities for the values that they might take in different circumstances. Best estimate here should ideally relate to some reasoned underlying view of the drivers, e.g. for liabilities sensitive to mortality this might include a best estimate of how mortality might improve through time. However, in places the computations mandated by Solvency II may not always be in line with how some might interpret the term ‘best estimate’ (e.g. the discount rates to be used are specified by Solvency II and so might not be in line with theoretical ‘best estimates’ bearing in mind the risks being expressed by the liabilities). Solvency II then makes the assumption that if a buyer were prepared to take on such liabilities from the original insurer then it would require some compensation for the basis risk between the overall replicating portfolio and the liabilities. Instead, there would be an additional component, called the ‘risk margin’ by Solvency II, corresponding to the additional premium another insurer might be expected to demand to take on such liabilities and being exposed to basis risk. The assumption is that such an insurer would typically need to set aside capital in addition to the best estimate computation, to protect itself against the risk that the best estimate might prove inaccurate. This capital would in turn need servicing which would increase the price that such an insurer would presumably want to charge for accepting this risk. In Solvency II this additional cost is determined by reference to the notional cost of servicing the additional capital as per the Solvency Capital Requirement (SCR) that would be introduced by having the liability on the new insurer’s books.Areas of disagreement
There are strongly held and differing views on how to interpret market consistency for certain types of liabilities (and assets) that are not readily traded on a market. It is not the purpose of this paper to express opinions on the validity of views expressed in these areas but we think it is worth highlighting in this paper what some of them are. However, we are of the opinion that any market consistent valuation framework has to have at least the properties we summarise in the conclusions below. Before doing so, it is worth making some general comments: (a) Different interpretations of market consistency in some of these areas could materially affect the capital adequacy position of some industry segments, which may partly explain why some views are strongly expressed. (b) Capital requirements under e.g. Solvency II depend not just on how a (market consistent) value is placed on the liabilities but also on how the firm’s (additional) solvency capital requirement (SCR) is calculated (and on how assets are valued and recognised in the solvency balance sheet). Some areas of disagreement correspond with differences of opinion over the risk characteristics being expressed by different types of liabilities. (c) In principle, the methodology used for MCV should depend on the purpose of the valuation. In the context of capital adequacy this is linked to the level of security it is considered that a given regulatory capital framework ‘ought’ to be targeting (and how the framework should react to changing economic conditions). Usually market consistent valuations are determined as if the liabilities due to policyholders are certain to be honoured by the insurer (although there can then be disagreements over what constitutes ‘certainty’, i.e. what is risk‐free, in this context). However, insurers are not certain to honour their liabilities to policyholders. Instead, policyholders have some credit risk exposure to their insurer. As noted by e.g. Kemp (2009) a more general formulation of market consistency would involve the MCV of a given liability (from the perspective of policyholders) being adjusted to reflect this credit exposure. Following usual credit risk pricing principles such an adjustment would show up as a credit spread adjustment applied to the discount rate that would otherwise be used to value the liabilities. More precisely, we may conceptually view a regulatory framework as targeting a specific (maximum) credit spread that ought to apply in such a computation if the insurer is to be deemed to be ‘adequately’ capitalised by the regulatory framework. This spread might perhaps change through time if we want the regulatory framework to exhibit counter‐cyclical features. So a full specification of an MCV (or more precisely the combination of the MCV and the SCR) requires some agreed view on how secure the promised liability ‘ought’ to be for any given type of firm and hence implicitly on the size of the credit spread adjustment referred to above. Some areas of disagreement correspond with differences of opinion on the sizes of adjustment that should be applied to ‘risk‐free’ rates for specific liability types (and hence, in practice, for specific industry segments). The areas that seem to have created the most disagreement to date over how to apply market consistent principles to the valuation of liabilities are probably: (1) Selection of the discount rate used to value liability cash flows that are longer in term than those of any readily traded assets.- Usually cash flows beyond a certain cut off are valued in a manner that depends in part on a presumed ‘ultimate forward rate’ (UFR), i.e. a discount rate that should be applied to an infinitely long liability. Ways in which disagreements manifest themselves include disputes over:
- What is the correct value to use for the UFR (for the relevant currency)?
- How rapidly should the discount rate trend towards the UFR beyond the selected cut‐ off?
- Is it reasonable to have a sharp cut‐off at a single term point, before which reliable market observable data is deemed to exist but after which it is deemed not to (and if so what should this term point be), or is it more appropriate to include a more gradual fading between existence and non‐existence of reliable market observables? Related to this are debates about whether a sharp cut‐off point gives inappropriately large weight to the reliability of data derived from the instrument which most closely corresponds to this cut‐off point and/or might lead to undesirable market behaviours or other macro‐prudential issues.
- Is it possible to have liabilities that have ‘exactly the same cash flow characteristics’ but are more liquid or is liquidity one of the inherent characteristics that need to be considered when identifying whether cash flows are ‘exactly the same’?
- How should an illiquid liability be defined?
- Can the use of an illiquidity premium be considered market consistent, since it implies a hold‐to‐maturity view of assets (or a static replication) and replication with illiquid assets that do not have reliable market prices? If the main reason for proposing it is to introduce counter‐cyclical behaviour into the overall regulatory framework then how effective (and workable) would it be at achieving this desired goal (and is this goal desirable) versus other potentially less desirable consequences it might also introduce?
- How should the quantum of liquidity (or illiquidity) expressed by a given asset or liability be defined? For example if the appropriate measure of liquidity is viewed as the length of time it might reasonably take to locate another party with whom a transaction at close to mid‐market price could be executed then perhaps liability and asset liquidity can be matched as long as these timescales are same. In contrast, if the appropriate measure of liquidity is viewed as the size of the bid‐offer spread that would be incurred were the asset or liability be liquidated then bid‐offer spreads are incurred both when entering and exiting a position, so asset illiquidity and liability illiquidity would then add rather than net off.
- All of the same topics as (2); and
- Should the (MCV) value of a liability depend on the assets held to back it (or more precisely the assets that the insurer merely currently intends to hold to back it) or should it be an intrinsic feature of the liability itself independent of the insurer’s asset portfolio? Irrespective of the intrinsic views a commentator may hold on this topic, they may also hold views on the practicality of any proposed methodology, as it will generally be simpler to carry out a computation that does not depend on the actual assets held in a specific portfolio.
Conclusions
In summary, market consistent valuations have the following characteristics:- The market consistent value of a financial instrument that is traded in a deep, liquid and transparent market equals its market value or price for which it may be exchanged in the market. Otherwise, arbitrage opportunities would be possible.
- The market consistent value of a liability is determined by the choice of assets that need to be used for the (dynamic) replication of the cash flows underlying the liability.
- The market consistent value of a liability is conceptually based on replication of that liability with assets that are traded in a deep, liquid and transparent market and thus for which reliable market prices can be observed.
- The cash flow of a financial instrument can always (conceptually) be unbundled into two components: (i) a component that can be perfectly (i.e. under all possible future states of the world) replicated by the replicating assets; and (ii) the remainder (the non‐replicable component).
- The market consistent value is then the market value of the portfolio of assets that replicates the first component plus a risk margin that is determined by the non‐replicable component.
- For regulatory purposes insurers have to hold capital to buffer the risk that the cash flows of its assets deviate from the cash flow of its liabilities over the lifetime of insurance liabilities. It is therefore natural for insurance liabilities to define an additional margin as the expected cost of capital to buffer the risk of the non‐replicable component of the insurance liability cash flow. This kind of risk margin is then also determined by the choice of replicating assets as well as by the insurance liabilities (and by the risks expressed by asset and liability portfolio of the insurer).





1 thought on “An actuarial view of market consistency”
Comments are closed.